Именно для таких «локальных» сценариев — когда нужно доказать корректность конкретной модели преобразования между двумя метамоделями (например, банковских сообщений) — использование Lean (или любого другого доказателя) оказывается куда более прямолинейным и реалистичным, чем попытки верифицировать целый язык вроде Rust вместе с оптимизирующим компилятором.
Ниже кратко опишу общий подход, как можно подступиться к задаче «доказать корректность трансформации из Метамодели A в Метамодель B» с помощью Lean.
1. Формальное описание метамоделей A и B в Lean
Синтаксические структуры.
Если в метамоделях A и B описываются сущности вроде «счет», «платёжка», «реквизиты получателя» и т. д., то в Lean вы описываете это через индуктивные типы (inductive) или структуры (structure) плюс взаимосвязи между ними.
Пример (очень упрощённый):
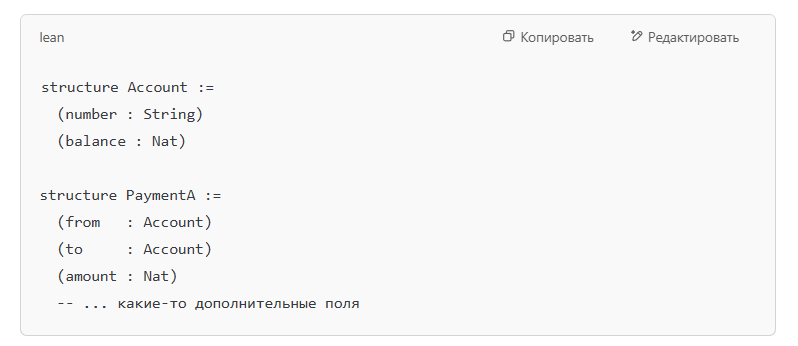
Аналогично для метамодели B.
Дополнительные ограничения и инварианты.
Часто метамодель содержит не только структуру, но и некие «бизнес-правила» (например, «сумма платежа не должна превышать баланс отправителя»). Эти правила можно формализовать как предикаты:

Аналогично задаются правила для объектов метамодели B.
Таким образом, вы получаете «чистую» формальную модель обеих метамоделей внутри Lean: структуры + набор свойств, которые должны выполняться (инварианты).
2. Задание самой трансформации (преобразования)
После того как A и B описаны, вы определяете функцию transform : A → B. Часто это будет не одна функция, а целый набор («mapping rules»), но в Lean их можно собрать в единый «трансформатор».
Например, если у вас есть PaymentA и вы хотите получить PaymentB, то в Lean это может выглядеть примерно так:
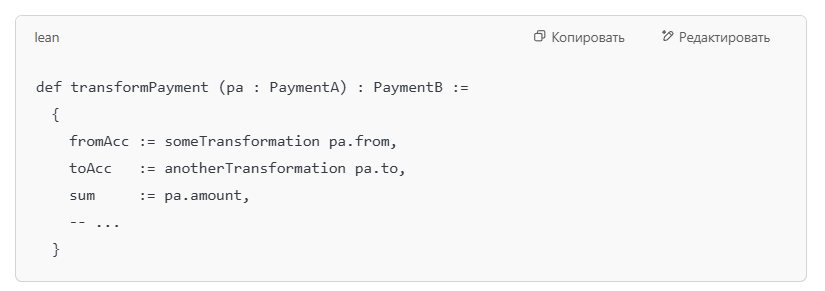
Или, если преобразование сложнее и зависит от разных условий, вы описываете это в виде pattern matching, рекурсий и т. д.
Важно, что вся логика маппинга формально зашита в Lean, а не «на словах». То есть вы получаете однозначное определение: какую структуру B порождает каждая структура A.
3. Определение критерия «валидности» трансформации
Чтобы что-то доказать, нужно формальное утверждение. Обычно хотят доказать, что:
Каждое валидное A-объект переходит в валидный B-объект.*
То есть, если isValidPaymentA pa истинно, тогда после трансформации let pb := transformPayment pa, должно выполняться isValidPaymentB pb.
Записывается как теорема:
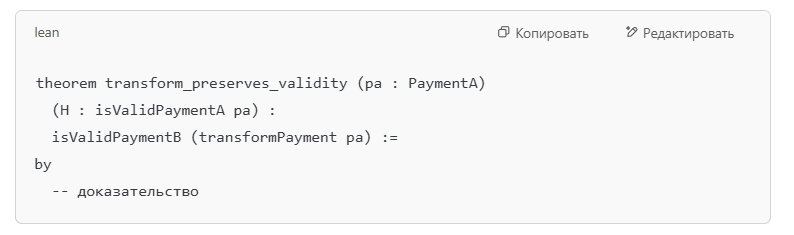
Дополнительные инварианты. Например, «сумма платежа сохраняется» или «идентификаторы счёта совпадают в нужных полях». Всё это вы формулируете как леммы или части основной теоремы:

Связь между разными объектами. Если речь идёт о цепочке сообщений (A_1, A_2, …), то вы можете утверждать, что «на выходе получается правильная последовательность B_1, B_2, …», и что все согласованные правила (например, остаток на счёте после перевода) соблюдены.
Главное, что точно вы хотите считать корректностью, зависит от вашей предметной области. Но в Lean это будет формулироваться как ∀ x, P(x) → Q(transform(x)) и вы будете доказывать это тактиками (proof scripts).
4. Процесс доказательства
Обычно доказательства в Lean строятся по схеме индукции (если структура рекурсивна) или пошаговыми рассуждениями.
Lean даёт вам тактики вроде intro, cases, induction, simp и т.д., которые помогают разбивать задачу на подслучаи и упрощать формулы.
В итоге вы получаете формальное подтверждение: для всех экземпляров A, удовлетворя isValidPaymentA, результат transformPayment в B будет удовлетворять isValidPaymentB.
Это именно то, чего обычно не хватает классическому MDD-подходу: там трансформации часто задаются в QVT или ATL, и мы ограничиваемся либо тестами, либо рассуждениями «на бумаге», что трансформация корректна. А в Lean можно получить машинно проверяемое доказательство.
5. Что дальше делать с Lean-трансформацией?
Исполнять прямо в Lean. Lean — это не только доказатель, но и (в Lean 4) полноценный язык, который может компилироваться в С/С++. При желании вы можете запускать трансформацию «вживую», если объёмы данных не слишком велики.
Экспортировать/переписать трансформацию в реальный продакшн-код. Если у вас большие объёмы и нужна быстрая интеграция, вы можете реализовать те же правила преобразования в Java или Rust, а потом (как в Cedar) использовать property-based тестирование и сравнивать результаты с Lean-реализацией на тысячах примеров. Формального 100% доказательства соответствия не будет, но практическая уверенность будет очень высокой.
Написать генератор (реже встречается) — автоматизировать перевод Lean-кода в другой язык. В Coq, Isabelle, Agda есть встроенные механизмы экспорта в Haskell/OCaml/Scala. У Lean 4 тоже появляются разные плагины, но это скорее экспериментальные вещи.
Краткий вывод
Да, для «локальных» задач вроде доказательства корректности конкретного преобразования (A→B) Lean подходит идеально.
Вы формализуете обе метамодели и само преобразование, формулируете критерии корректности (инварианты), и доказываете, что для всех корректных A-объектов результат в B тоже корректен (или сохраняет нужные свойства).
Это гораздо проще, чем пытаться верифицировать всю инфраструктуру (язык, компилятор и т.д.).
Таким образом, Lean действительно может заменить MOF + «неформальные» описания трансформаций, дав вам возможность строгих доказательств корректности модели.
Если затем потребуется «промышленная» реализация, обычно комбинируют:
Теоремы в Lean,
Реальный код + миллионы тестов против Lean-модели (либо ручной аудит).
Но уже сам факт формализованной модели даёт большой выигрыш для уверенности и понимания, что ваша трансформация соответствует заявленным инвариантам.